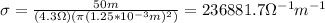Question

A current of 5 A exists in a copper wire of length 50 m and diameter of 2.5 mm when applying a

potential difference of 0.86 V. Assuming the current is uniform, calculate
(a) the current density
(b) electron drift speed.
(c) the copper conductivity​

Answer 1

a) 1273.23 A/m^2

b) 7.19*10^-5 m/s

c) 236881.7 Ohms

Step-by-step explanation:

(a) To find the current density you use the following formula:

`J=(I)/(A)=(I)/(\pi r^2)`

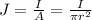
I: current in the wire

A: cross area of the wire

r: radius of the wire

`J=(5A)/(\pi(1.25*10^(-3)m)^2)=1273.23(A)/(m^2)`

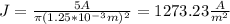
(b) The electron drift speed is given by:

`v_d=(I)/(nqA)=(I)/(nq\pi r^2)`

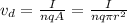
n: number of conduction electrons per m^3

q: charge of the electron = 1.6*10^-19C

The number of free electrons is calculated by using:

`n=(\rho N_A)/(M)\\\\n=((9*10^(3)kg/m^3)(6.22*10^(23)))/(63.54*10^(-3))=8.5*10^(28)`

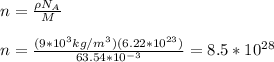
Next, you replace the values of the parameters in the equation for vd:

`v_d=(5A)/((8.85*10^(28)m^(-3))(1.6*10^(-19)C)\pi (1.25*10^(-3)m)^2)\\\\v_d=7.19*10^(-5)(m)/(s)`

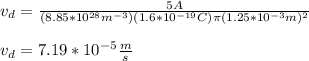
(c) The conductivity is given by:

`\sigma=(L)/(RA)`

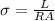
You first calculate R:

`R=VI=(0.86V)(5A)=4.3\Omega`

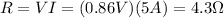
Next, replace for sigma:

`\sigma=(50m)/((4.3\Omega)(\pi (1.25*10^(-3)m)^2))=236881.7\Omega^(-1)m^(-1)`