Question

Mass hangs from a helical spring. The

periodic time of free vibration in a vertical
direction is 1.25sec. When the mass is at rest the
upper end of the spring is made to move with an
upward displacement of such that y=5 sin 2pt cm,
(t being the time in second measured from the
beginning of motion). Through what height is the
mass raised in the first 0.4 second? Find also the
amplitude of motion of the mass for steady state
vibration.

Answer 1

2.94 cm

20 cm

Step-by-step explanation:

Solution:-

- We are to consider a mass-spring system that initially undergoes free vibrations with a time period ( T ) given to be 1.25s.

- The natural frequency (w_n) of the free vibrations undergone by the system can be determined as:

`w_n = (2\pi )/(T) \\\\w_n = (2\pi )/(1.25)\\\\w_n = 5.02654(rad)/(s)`

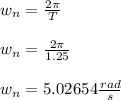
- The system is later excited with a base displacement of the form:

y ( t ) = Y*sin ( w*t )

- The upper end of the spring is made to move with the following displacement function:

y ( t ) = 5*sin (2π*t)

Where,

Y : The amplitude of excitation = 5

w : The excited frequency = 2*π

- The amount of height raised of the center of mass in the first 0.4 seconds can be determined from the excitation displacement ( y ( t ) ).

- The simple plugging of the t = 0.4 s in the displacement of function " y ( t ) ", hence:

`y ( 0.4 ) = 5*sin (2\pi *0.4)\\\\y ( 0.4 ) = 5*sin (2.51327)\\\\y ( 0.4 ) = 2.94 cm`

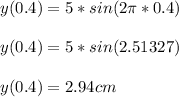
Answer: There will be a rise of 2.94 cm of the mass in the first 0.4 seconds.

- The equation of motion for the base excitation of mass-spring-damper system is given as follows:

`m*(d^2x)/(dt^2) + c*(dx)/(dt) + kx = k*y(t) + c*(dy)/(dt)`

Where,

m: The mass of the object ( point mass )

c : The viscous damping coefficient

k: The spring stiffness constant

x : The absolute motion of mass ( free vibration + excitation )

- For undamped system ( ζ = 0 ) i.e the damping coefficient ( c ) is zero. The complete solution of the mass-spring system is given in the form:

`m*(d^2x)/(dt^2) + kx = k*y(t) \\\\(d^2x)/(dt^2) + w_n^2*x = w_n^2*y(t)`

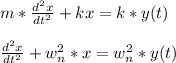
Where,

`w_n^2 = (k)/(m)`

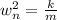
- The steady solution of an undamped mass-spring system is given in the form:

`x_s_s ( t ) = X_o sin ( w*t )`

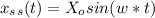
Where,

X_o : The amplitude of the mass for steady-state vibration.

- The general amplitude ( X_o ) for a damped system is given by the relation:

`X_o = Y*\sqrt{(1 + ( 2*p*r )^2)/(( 1 - r ) ^2 + ( 2*p*r )^2) }`

Where,

Y: The amplitude of exciting displacement ( y ( t ) )

p = ζ ( Damping ratio constant )

`r = (w)/(w_n) = (2*\pi )/((2\pi )/(T) ) = T= 1.25`

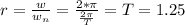
- The undamped system ( ζ = 0 ) i.e the damping coefficient ( c ) is zero. The amplitude ( X_o ) of a steady state response is given as:

`X_o = Y*\sqrt{(1 + ( 2*0*r )^2)/(( 1 - r ) ^2 + ( 2*0*r )^2) }\\\\X_o = Y*\sqrt{(1 )/(( 1 - r ) ^2 ) }\\\\X_o = Y*(1)/(1-r)`

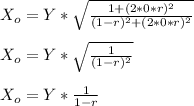
- Plug in the value of ( r ) and evaluate the amplitude of steady state response of the mass-spring vibration.

`X_o = 5*\sqrt{(1)/((1-1.25)^2) } \\\\X_o = 5*\sqrt{(1)/(0.0625) }\\\\X_o = 20 cm`

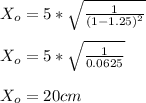
Answer: The steady state amplitude of the mass vibrations is ( X_o ) = 20 cm