Question

HELP PLS Which expression is equivalent to ( log 9 + 1/2 log x + log (x cubed + 4) - log 6?

Answer 1

Answer: C

Explanation:

I took the quiz

Answer 2

log [ (3/2) *
`√(x)` * (
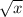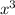`x^(3)` + 4) ] = ( log 9 + 1/2 log x + log (x cubed + 4) - log 6 )

Explanation:

I do not see answer choices, but I will simplify this expression.

( log 9 + 1/2 log x + log (x cubed + 4) - log 6 )

= log 9 - log 6 + 1/2 log x + log (x cubed + 4)

= log (9/6) + 1/2 log x + log (x cubed + 4),

I simply used the Quotient Rule for Logs

= log (9/6) + 1/2 log x + log (x cubed + 4),

= log (3/2) + 1/2 log x + log (x cubed + 4),

= log (3/2) + log x^(1/2) + log (x cubed + 4),

Power Rule for logs

= log (3/2) + log x^(1/2) + log (x cubed + 4),

= log ( (3/2)* x^(1/2) * (x cubed + 4) )

Applying Product Rule for Logs

= log ( (3/2)* x^(1/2) * (x cubed + 4) )

= log [ (3/2) *
`√(x)` * (
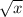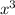`x^(3)` + 4) ]