Question

What is the length of AC?

Answer 1

Length of AC = 12units.

Explanation:

`\sf\large{\star Given:-}`

• Hypotenuse of the triangle =
  `\sf\pink{10\:units.}`
• Height of the triangle =
  `\sf\pink{8 \: units.}`

`\sf\large{\star To\: Find:-}`

`\rightarrow` Base of the triangle.

`\sf\large{\star Solution:-}`

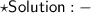
`\rightarrow`As we know that,

Pythagoras Theorem:

`\sf\blue{Hypotenuse^2\:=\: Height^2+Base^2}`

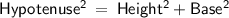
So, In triangle ABD by putting the value of hypotenuse and height in this formula we get,

`\rightarrow`
`\sf{10^2\:=\: 8^2 + Base^2}`

`\rightarrow`
`\sf{100\:=\: 64 + Base^2}`

`\rightarrow`
`\sf{100-64\:=\: Base^2}`

`\rightarrow`
`\sf{36\:=\: Base^2}`

`\rightarrow`
`\sf{√(36)\:=\: Base}`

`\rightarrow`
`\sf{6\:=\: Base}`

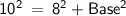
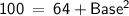
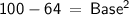
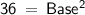
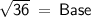
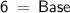
Since, it is given that BD is the perpendicular bisector of AC so length of AC will be doubled.

Therefore, length of AC of the given triangle =
`\sf\purple{12units.}`