Answer:
1.36 × 10³ mL of water.
Step-by-step explanation:
We can utilize the dilution equation. Recall that:
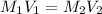
Where M represents molarity and V represents volume.
Let the initial concentration and unknown volume be M₁ and V₁, respectively. Let the final concentration and required volume be M₂ and V₂, respectively. Solve for V₁:
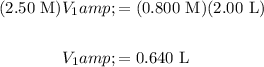
Therefore, we can begin with 0.640 L of the 2.50 M solution and add enough distilled water to dilute the solution to 2.00 L. The required amount of water is thus:
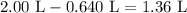
Convert this value to mL:
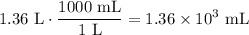
Therefore, about 1.36 × 10³ mL of water need to be added to the 2.50 M solution.