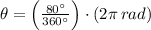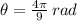Question

PLEASE PLEASE PLEASE HELP!!!!!!

In the following diagram, the radius of the outer circle is 8 cm and the radius of the inner circle is 4 cm. Find the following;

Answer 1

(See explanation for further details)

Explanation:

1) The circumference of the outer circle is:

`s_(EXT) = 2\pi\cdot (8\,cm)`

`s_(EXT) = 16\pi\,cm`

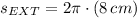
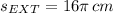
2) The circumference of the inner circle is:

`s_(INT) = 2\pi\cdot (4\,cm)`

`s_(INT) = 8\pi\,cm`

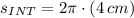
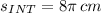
3) The area of the outer circle is:

`A_(EXT) = \pi\cdot (8\,cm)^(2)`

`A_(EXT) = 64\pi\,cm^(2)`

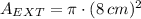
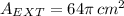
4) The area of the inner circle is:

`A_(INT) = \pi\cdot (4\,cm)^(2)`

`A_(INT) = 16\pi\,cm^(2)`

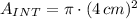
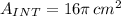
5) The length of the arc BC is:

`s_(BC) = \left((80^(\circ))/(360^(\circ)) \right)\cdot (16\pi\,cm)`

`s_(BC) = (32\pi)/(9)\,cm`

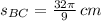
6) The length of the arc ST is:

`s_(ST) = \left((80^(\circ))/(360^(\circ)) \right)\cdot (8\pi\,cm)`

`s_(ST) = (16\pi)/(9)\,cm`

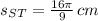
7) The area of the sector BPC is:

`A_(BPC) = \left((80^(\circ))/(360^(\circ)) \right)\cdot (64\pi\,cm^(2))`

`A_(BPC) = (128\pi)/(9)\,cm^(2)`

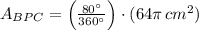
8) The area of the sector SPT is:

`A_(SPT) = \left((80^(\circ))/(360^(\circ)) \right)\cdot (16\pi\,cm^(2))`

`A_(SPT) = (32\pi)/(9)\,cm^(2)`

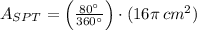
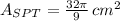
9) The radian measure of the sector BPC is:

`\theta = \left((80^(\circ))/(360^(\circ))\right)\cdot (2\pi\,rad)`

`\theta = (4\pi)/(9)\,rad`

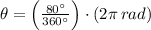
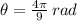
10) The radian measure of the sector SPT is::

`\theta = \left((80^(\circ))/(360^(\circ))\right)\cdot (2\pi\,rad)`

`\theta = (4\pi)/(9)\,rad`