Answer:
The distance difference between those swings is 20.6, approximately.
Explanation:
To find the difference between the distance of each swing, we need to subtract vectors and find the module of the resulting vector.
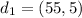 represents the first swing.
represents the first swing.
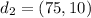 represents the second swing.
represents the second swing.
In the image attached, the difference is shown by vector
 .
.
Mathematically, this displacement is defined
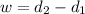

Now, we find its module
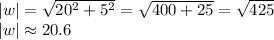
Therefore, the distance difference between those swings is 20.6, approximately.