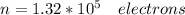Question

A model of a red blood cell portrays the cell as a spherical capacitor -- a positively charged liquid sphere of surface area A separated from the surrounding negatively charged fluid by a membrane of thickness t. Tiny electrodes introduced into the interior of the cell show a potential difference of 100 mV across the membrane. The membrane's thickness is estimated to be 95 nm and its dielectric constant is 5.00.

(a) If an average red blood cell has a mass of 1.00 10-12 kg, estimate the volume of the cell and thus find its surface area. The density of blood is 1100 kg/m3.
volume = 9.09e-16 m3
surface area = 4.548e-10 m2
(b) Estimate the capacitance of the cell.______ F
(c) Calculate the charge on the surface of the membrane._________ C
How many electronic (elementary) charges does the surface charge represent? _____

Answer 1

Step-by-step explanation:

Given that :

Mass of the red blood cell m=
`1.00*10^(-12) \ kg\\`

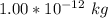
Density of the blood P = 1100 kg/m³

Dielectric constant K = 5.00

Potential Difference
`\Delta V = 100 mV` = 100×10⁻³ V

Thickness d = 95 nm = 95 × 10⁻⁹ m

Permittivity of free space
`\epsilon_o` =
`8.85 *10^(-12) C^2/N.m^2`

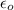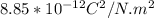
a)

the volume of the cell and thus find its surface area.

The volume of the cell is being calculated as follows:

`V = (m)/(\rho) \\ \\ = (1.00*10^(-12))/(1100 ) \\ \\ = 9.09*10^(-16) m^3`

Here the model of the red blood cell depicts that the cell is a spherical capacitor. Thus , the volume of the sphere is:

`V = (4)/(3) \pi r^3 \\ \\ r^3 = (3V)/(4 \pi ) \\ \\ r = ((3V)/(4 \pi))^(1/3)`

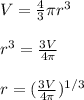
The radius of the sphere is =
`[(3(9.09*10^(-14) m^3))/(4 \pi) ]^{(1/3)`

= 6.01654×10⁻⁴ m

The surface area of the cell is A = 4 πr²

= 4 π ( 6.01654×10⁻⁴)²

= 4.548×10⁻¹⁸ m²

b) Estimate the capacitance of the cell.______ F

the capacitance of the cell ;

C =
`( \epsilon_o *A)/(d)`

C =
`((5.00)(8.85*10^(-12)*4.548*10^(-10))/(95*10^(-9))`

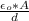
C = 2.11 × 10⁻¹³ F

c) Calculate the charge on the surface of the membrane._________ C

How many electronic (elementary) charges does the surface charge represent? _____

The charge on the surface of the membrane is given by:

`Q = C( \Delta V) \\ \\ Q =2.11*10^(-13) *100*10^(-3) \\ \\ Q = 2.11*10^(-14) C`

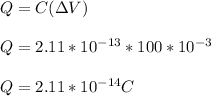
the numbers of electrons in the surface of the charge is :

`n = (Q)/(e) \\ \\ where\ \ e = .602*`10^(-19) \ C \\ \\ n = (2.11*10^(-14)C)/(1.602*10^(-19))`

`n = 1.32*10^5 \ \ \ electrons`