Question

In the Changing Dimensions of 3D Figures

section, if a prisms dimensions were
changed by a scale factor of 3, how would
the surface area change?*
O
It would stay the same
O
It would change by a scale factor of 3.
It would change by a scale factor of 6.
O
It would change by a scale factor of 9.
O
It would change by a scale factor of 27.

Answer 1

facter of 9 (people with ads)

Explanation:

Answer 2

Answer:factor of 9

Explanation:

Given

prism were changed by a scale factor of 3

Suppose prism is rectangular in shape

So surface are is
`S.A.=2(lw+wb+lb)`

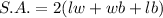
Where l=length

w=width

b=breadth

So new length,breadth and width is

`l'=3l`

`w'=3w`

`b'=3b`

`S.A.=2(3* 3lw+3* 3wb+3* 3lb)`

`S.A.=2* 3^2(lw+wb+lb)`

`S.A.=3^2* 2(lw+wb+lb)`

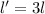
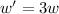
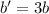
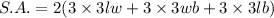
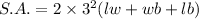
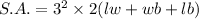
So new surface area would change by a factor of 9