Question

A ball has a volume of 6.35 liters and is at a temperature of

27.0°C. A pressure gauge attached to the ball reads 0.45
atmosphere. The atmospheric pressure is 1.00 atmosphere.
Calculate the absolute pressure inside the ball and the
amount of moles of air it contains. (First, find the absolute
pressure and then use that to find the moles using the ideal
gas law. Remember to use the correct ideal gas constant and
to convert from celsius to kelvin.)

Answer 1

• Absolute pressure inside the ball:
  `1.45\; \rm atm`.
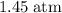• Number of moles of air particles inside the ball, by the ideal gas law: approximately
  `0.37\; \rm mol`.

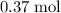Step-by-step explanation:

The gauge pressure inside the ball gives the absolute pressure inside the ball, relative to the atmospheric pressure outside the ball. In other words:

`\begin{aligned}& \text{Gauge Pressure} \\ &= \text{Absolute Pressure} - \text{Atomspheric Pressure}\end{aligned}`.

Rearrange to obtain:

`\begin{aligned}& \text{Absolute Pressure} \\ &= \text{Gauge Pressure} + \text{Atomspheric Pressure} \\ &= 0.45\; \rm atm + 1.00 \; \rm atm = 1.45\; \rm atm\end{aligned}`.

Look up the ideal gas constant. This constant comes in a large number of unit combinations. Look for the one that takes
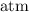`\rm atm` for pressure and
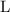`\rm L` for volume.

`R = 0.082057\; \rm L \cdot atm \cdot K^(-1)\cdot mol^(-1)`.

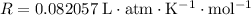Convert the temperature to absolute temperature:

`T = 27.0\; \rm ^\circ C \approx (27.0 + 273.15)\; \rm K = 300.15\; \rm K`.

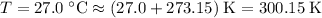Assume that the gas inside this ball acts like an ideal gas. Apply the ideal gas law
`P \cdot V = n \cdot R \cdot T` (after rearranging) to find the number of moles of gas particles in this ball:

`\begin{aligned}n &= (P \cdot V)/(R \cdot T) \\ &= (1.45\; \rm atm * 6.35\; \rm L)/(0.08205 \; \rm L \cdot atm \cdot K^(-1) \cdot mol^(-1) * 300.15\; \rm K) \approx 0.37\; \rm mol\end{aligned}`.

(Rounded to two significant figures, as in the pressure gauge reading.)