Question

The manager of a computer retails store is concerned that his suppliers have been giving him laptop computers with lower than average quality. His research shows that replacement times for the model laptop of concern are normally distributed with a mean of 4.3 years and a standard deviation of 0.4 years. He then randomly selects records on 27 laptops sold in the past and finds that the mean replacement time is 4.1 years.

Assuming that the laptop replacment times have a mean of 4.5 years and a standard deviation of 0.5 years, find the probability that 32 randomly selected laptops will have a mean replacment time of 4.3 years or less.
P(M < 4.3 years) =
Enter your answer as a number accurate to 4 decimal places. NOTE: Answers obtained using exact z-scores or z-scores rounded to 3 decimal places are accepted.
Based on the result above, does it appear that the computer store has been given laptops of lower than average quality?

Answer 1

P(z ≤ -2.263) = 0.012 ( 3 dp)

Yes, the computer store has been given laptops of lower than average quality. The probability is unlikely to have occurred by chance.

Explanation:

Sample size, n = 32

Mean,
`\mu = 4.5`

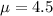
Standard deviation,
`\sigma = 0.5`

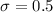
Sample mean,
`M = 4.3`

`z = (M - \mu)/(\sigma / √(n) ) \\z = (4.3 - 4.5)/(0.5 / √(32) )`

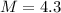
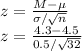
z = - 2.263

Probability that the selected laptops will have a mean replacement time of 4.3 years or less.

P(M ≤ 4.3 years) = P(z ≤ -2.263)

P(z ≤ -2.263) = 0.0118

P(z ≤ -2.263) = 0.012 ( 3 dp)

P(z ≤ -2.263) = 0.012 is less than 0.05 significant level, it is safe to conclude that the computer store has been given laptops of lower than average quality