Question

The three series ∑An,∑Bn, and ∑Cn have the terms An=1/n^8 , Bn=1/n^5 , Cn=1/n. Use the Limit Comparison Test to compare the following series to any of the above series. For each of the series below, you must enter two letters. The first is the letter (A,B, or C) of the series above that it can be legally compared to with the Limit Comparison Test. The second is C if the given series converges, or D if it diverges. So for instance, if you believe the series converges and can be compared with series C above, you would enter CC; or if you believe it diverges and can be compared with series A, you would enter AD.

[infinity]
a. ∑n=1 5n^2+8n^7/ 5n^8 + 6n^3-5

[infinity]
b. ∑n=1 8n^4+ n^2 -8n/ 6n^12 -5n^10 + 8

[infinity]
c. ∑n=1 5n^5+ n^8/ 149n^13+ 6n^5 + 5

Answer 1

Case a) CD

Case b) AC

Case c) BC

Explanation:

Notice that the three series given: A, B and C, are examples of what is referred as "p-series". These type of series are of the form:

`\sum\limits^\infty_1 {(1)/(n^p)}}\\`

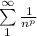
which converge if p>1 and diverge otherwise.

Therefore, we know that the series:

`A=\sum\limits^\infty_1 (1)/(n^8)` converges since p = 8 in this case

`B=\sum\limits^\infty_1 (1)/(n^5)` converges since p = 5 for this case

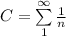`C=\sum\limits^\infty_1 (1)/(n)` diverges since p = 1 (this is the famous "harmonic Series")

Now we study the first series of polymonial quotient

Case a)
`\sum\limits^\infty_1 (5n^2+8n^7)/(5n^8+6n^3-5)\\`

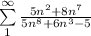
We write both polynomials in numerator and denominator in standard form to compare their leading terms:

`(5n^2+8n^7)/(5n^8+6n^3-5)=(8n^7+5n^2)/(5n^8+6n^3-5)`

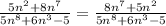
Comparing leading terms, we get:

`(8n^7)/(5n^8)=(8)/(5) (1)/(n)`

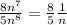
So since it behaves like the harmonic series, we are going to use the Limit Comparison Test with the Harmonic series:

`\lim_(n \to \infty) ((8n^7+5n^2)/(5n^8+6n^3-5) )/((1)/(n) ) = \lim_(n \to \infty) (8n^8+5n^3)/(5n^8+6n^3-5) } =(8)/(5) \\`

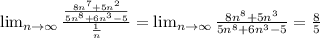
This is a finite and positive number, and therefore, this series for case a) must diverge as the Harmonic series does. As per the requested convention, we write: CD (use series C as comparison and showing that it diverges)

Case b)
`\sum\limits^\infty_1 (8n^4+n^2-8n)/(6n^(12)-5n^(10)+8)\\`

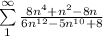
We then compare their leading terms:

`(8n^4)/(6n^(12))=(4)/(3) (1)/(n^8)`

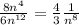
So since it behaves like series "A", we are going to use the Limit Comparison Test with the given converging A series:

`\lim_(n \to \infty) ((8n^4+n^2-8n)/(6n^(12)-5n^(10)+8) )/((1)/(n^8) ) = \lim_(n \to \infty) (8n^(12)+n^(10)-8n^9)/(6n^(12)-5n^(10)+8) } =(8)/(6) =(4)/(3) \\`

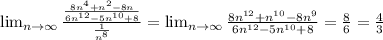
This is a finite and positive number, and therefore, this series for case b) must converge as series A does. As per the requested convention, we write: AC (use series A as comparison and showing that it converges)

Case c)
`\sum\limits^\infty_1 (n^8+5n^5)/(149n^(13)+6n^(5)+5)\\`

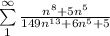
We then compare their leading terms:

`(n^8)/(149n^(13))=(1)/(149) (1)/(n^5)`

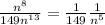
So since it behaves like series "B", we are going to use the Limit Comparison Test with the given converging B series:

`\lim_(n \to \infty) ((n^8+5n^5)/(149n^(13)+6n^(5)+5) )/((1)/(n^5) ) = \lim_(n \to \infty) (n^(13)+5n^(10))/(149n^(13)+6n^(5)+5) } =(1)/(149)`

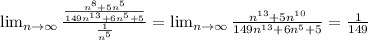
This is a finite and positive number, and therefore, this series for case c) must converge as series B does. As per the requested convention, we write: BC (use series B as comparison and showing that it converges)