Question

In 2008, the average household debt service ratio for homeowners was 12.9. The household debt service ratio is the ratio of debt payments (such as mortgage payments) to disposable personal income. You are asked to evaluate this debt ratio for the last 10 years using a random sample of 44 Americans with a mean of 13.88 and a standard deviation of 3.14.

1. Can you infer that the debt service ratio has increased since 2008? Use α = 0.05.
2. Report the value of the test statistics and critical value or p-value

Answer 1

We conclude that the debt service ratio has increased since 2008.

Explanation:

We are given that in 2008, the average household debt service ratio for homeowners was 12.9.

You are asked to evaluate this debt ratio for the last 10 years using a random sample of 44 Americans with a mean of 13.88 and a standard deviation of 3.14.

Let
`\mu` = average household debt service ratio after 10 years.

So, Null Hypothesis,
`H_0` :
`\mu` = 12.9 {means that the debt service ratio has not increased since 2008}

Alternate Hypothesis,
`H_A` :
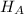`\mu` > 12.9 {means that the debt service ratio has increased since 2008}

The test statistics that would be used here One-sample t test statistics as we don't know about population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n)))` ~
`t_n_-_1`

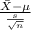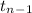
where,
`\bar X` = sample mean debt ratio = 13.88

s = sample standard deviation = 3.14

n = sample of Americans = 44

So, test statistics =
`(13.88-12.9)/((3.14)/(√(44)))` ~
`t_4_3`

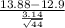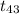
= 2.07

The value of t test statistics is 2.07.

Now, at 0.05 significance level the t table gives critical value of 1.682 at 43 degree of freedom for right-tailed test. Since our test statistics is more than the critical values of t, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the debt service ratio has increased since 2008.