Question

An engineer is comparing voltages for two types of batteries (K and Q) using a sample of 72 type K batteries and a sample of 49 type Q batteries. The mean voltage is measured as 9.41 for the type K batteries with a standard deviation of 0.723, and the mean voltage is 9.69 for type Q batteries with a standard deviation of 0.257. Conduct a hypothesis test for the conjecture that the mean voltage for these two types of batteries is different. Let µ1 be the true mean voltage for type K batteries and µ2 be the true mean voltage for type Q batteries. Use α = 0.05 level of significance.

1. State the null and alternative hypotheses for the test.
2. Compute the value of the test statistic. Round your answer to two decimal places.
3. Determine the decision rule for rejecting the null hypothesis H0. Round the numerical portion of your answer to two decimal places.
4. Make the decision for the hypothesis test.

Answer 1

Given:

For battery k(sample 1):

Sample size, n = 75

Sample mean, X' = 9.41

Standard deviation = 0.723

Mean u1 =???

For battery Q(sample 2):

Sample size, n = 49

Sample mean, X' = 9.69

Standard deviation = 0.257

Mean u2 =???

Significance level = 0.05

1) The null and alternative hypotheses, will be given as:

H0 : u1 - u2 = 0

H1 : u1 - u2 ≠ 0

2) This is a two tailed test.

For the test statistic, we have :

`Z_o = \frac{X'_1 - X'_2}{\sqrt{((\sigma_1)^2)/(n_1) + ((\sigma_2)^2)/(n_2)}}`

`= \frac{9.41 - 9.69}{\sqrt{((0.723)^2)/(75) + ((0.257)^2)/(49)}} = - 3.018`

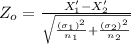
≈ 3.02

The Zo = - 3.02

3) For the p value, using excel, we have:

2 * P(Z > (-3.018))

= 2 * NORMDIST (-3.018, 0, 1, true)

= 0.00254

For critical value:

Zcritical = Za/2 = 0.05/2

Zcritical = 0.025

We have alternative hypothesis,

H1 : u1 - u2 ≠ 0.

Therefore we reject null hypothesis H0 if Zo > Zcritical

4) We reject null hypothesis H0 if Zo > Zcritical. At 0.05 level of significance, there is not enough evidence to conclude that mean u1 and mean u2 are different.