Question

A study of female entrepreneurs was conducted to determine their definition of success. The women were offered optional choices such as happiness/self-fulfillment, sales/profit, and achievement/challenge. The women were divided into groups according to the gross sales of their businesses. A significantly higher proportion of female entrepreneurs in the $100,000 to $500,000 category than in the less than $100,000 category seemed to rate sales/profit as a definition of success. Suppose you decide to test this result by taking a survey of your own and identify female entrepreneurs by gross sales. You interview 100 female entrepreneurs with gross sales of less than $100,000, and 24 of them define sales/profit as success. You then interview 95 female entrepreneurs with gross sales of $100,000 to $500,000, and 39 cite sales/profit as a definition of success.

1. Use this information to test to determine whether there is a significant difference in the proportions of the two groups that define success as sales/profit. Use α = .05.
2. Calculate the value of the test statistics.
3. Calculate the p-value.

Answer 1

We conclude that there is a significant difference in the proportions of the two groups that define success as sales/profit.

Explanation:

We are given that a study of female entrepreneurs was conducted to determine their definition of success.

You interview 100 female entrepreneurs with gross sales of less than $100,000, and 24 of them define sales/profit as success. You then interview 95 female entrepreneurs with gross sales of $100,000 to $500,000, and 39 cite sales/profit as a definition of success.

Let
`p_1` = proportion of female entrepreneurs with gross sales of less than $100,000 who define sales/profit as success.

`p_2` = proportion of female entrepreneurs with gross sales of $100,000 to $500,000 who define sales/profit as success.

So, Null Hypothesis,
`H_0` :
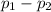`p_1-p_2` = 0 {means that there is no significant difference in the proportions of the two groups that define success as sales/profit}

Alternate Hypothesis,
`H_A` :
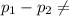`p_1-p_2\\eq` 0 {means that there is a significant difference in the proportions of the two groups that define success as sales/profit}

The test statistics that would be used here Two-sample z proportion statistics;

T.S. =
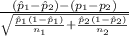`\frac{(\hat p_1-\hat p_2)-(p_1-p_2)}{\sqrt{(\hat p_1(1-\hat p_1))/(n_1)+(\hat p_2(1-\hat p_2))/(n_2) } }` ~ N(0,1)

where,
`\hat p_1` =
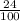`(24)/(100)` = 0.24

`\hat p_2` =
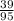`(39)/(95)` = 0.41

`n_1` = sample of female entrepreneurs with gross sales of less than $100,000 = 100

`n_2` = sample of female entrepreneurs with gross sales of $100,000 to $500,000 = 95

So, test statistics =
`\frac{(0.24-0.41)-(0)}{\sqrt{(0.24(1-0.24))/(100)+(0.41(1-0.41))/(95) } }`

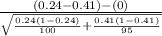
= -2.57

The value of z test statistics is -2.57.

Also, P-value of test statistics is given by;

P-value = P(Z < -2.57) = 1 - P(Z
`\leq` 2.57)

= 1 - 0.99492 = 0.0051

Now, at 0.05 significance level the z table gives critical values of -1.96 and 1.96 for two-tailed test.

Since our test statistics doesn't lie within the range of critical values of z, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that there is a significant difference in the proportions of the two groups that define success as sales/profit.