Question

Find the rate of change for f(x)=x^2-8x+15 from x=0 to x=4

Answer 1

-4

Explanation:

Find the rate of change for f(x) = x² - 8x + 15 from x = 0 to x = 4

The rate of change is the rate at which a variable changes over a specific period of time.

Averate rate of change:
`(f(b)-f(a))/(b-a)`

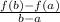
First, we need to find the functions for when x = 0 and when x = 4:

For x = 0

f(x) = x² - 8x + 15

f(0) = 0² - 8(0) + 15

f(0) = 0 - 0 + 15

f(0) = 15

For x = 4

f(x) = x² - 8x + 15

f(4) = (4)² - 8(4) + 15

f(4) = 16 - 32 + 15

f(4) = -16 + 15

f(4) = -1

Averate rate of change:
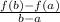
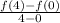
`(f(b)-f(a))/(b-a)`

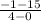
A =
`(f(4)-f(0))/(4-0)`

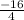
A =
`(-1-15)/(4-0)`

A =
`(-16)/(4)`

A =
`-4`

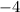
Therefore, the rate of change from x = 0 to x = 4 is -4.

Hope this helps!