Question

Suppose that an accounting firm does a study to determine the time needed to complete one person's tax forms. It randomly surveys 175 people. The sample mean is 22.1 hours. There is a known population standard deviation of 6.0 hours. The population distribution is assumed to be normal. NOTE: If you are using a Student's t-distribution, you may assume that the underlying population is normally distributed. (In general, you must first prove that assumption, though.)

Part (a)
(i)´x=______
(ii)σ=______
(iii)σ´x=______(rounded to three decimal places)
(iv)n=______
(v)n− 1 =______
Part (b)
Define the Random Variables X and´x in words.
a. X is the number of tax forms that an accounting firm completes, and´x is the average number of tax forms that an accounting firm completes.
b. X is the time needed to complete a person's tax forms, and´X is the average time needed to complete 200 tax forms.
c. X is the number of tax forms that an accounting firm completes, and X is the average number of tax forms that an accounting firm completes.

Answer 1

Part (a)

i) 'x⁻' = 22.1 hours

ii) 'σ' = 6.0 hours

iii) σₓ = 0.453

iv) n =175

v) n-1 = 175-1 =174

Part(b):- option (a)

X is the number of tax forms that an accounting firm completes, and ´x is the average number of tax forms that an accounting firm completes

Explanation:

Explanation:-

Given the sample size 'n' = 175 people

Given the sample mean 'x⁻' = 22.1 hours

Given the Population standard deviation 'σ' = 6.0 hours

sample standard deviation =

σₓ =
`(S.D)/(√(n) ) = (6)/(√(175) ) =0.453`

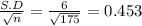
Part (a)

i) 'x⁻' = 22.1 hours

ii) 'σ' = 6.0 hours

iii) σₓ = 0.453

iv) n =175

v) n-1 = 175-1 =174

Part(b)

Answer:- ( a)

X is the number of tax forms that an accounting firm completes, and ´x is the average number of tax forms that an accounting firm completes