Question

A test is conducted to determine the overall heat transfer coefficient in a shell-and-tube oil-to-water heat exchanger that has 24 tubes of internal diameter 1.2 cm and length 3 m in a single shell. Cold water (cp = 4180 J/kg·K) enters the tubes at 20°C at a rate of 3 kg/s and leaves at 55°C. Oil (cp = 2150 J/kg·K) flows through the shell and is cooled from 120°C to 45°C. Determine the overall heat transfer coefficient Ui of this heat exchanger based on the inner surface area of the tubes.

Answer 1

U = 5.53 kW/m² °C

Step-by-step explanation:

Given:

N = 24

L = 3m

Di = 1.2 cm = 0.012m

For water:

m = 3 kg/s; Twin = 20°C; Twout= 55°C

Cp = 4180 J/kg·K

For oil:

To_in= 120°C; To_out = 45°C;

For change in temperature

ΔT1 = To_in - Twout

120° - 55° = 65°C

ΔT2 = To_out - Twin

= 45 - 20 = 25°C

For the rate of heat transfer from water to oil:

Q = m*Cp(Twout - Twin)

Q = (3kg/s)*(4180J/kg.k)(55°C -20°C)

Q = 439800 ≈ 439.8 KW

The total surface area, A, of the tube =

A = N*pi*Di*L

A = 24*3.142*0.012*3

A = 2.714m²

Let's find the overall transfer coefficient, U, using the formula :

Q = U * A * F * ΔTlm

Where F= correction factor.

ΔTlm = logarithmic mean temperature

Average temperature difference =

`\delta T_lm = (\delta T_1 - \delta T_2)/(ln [(\delta T_1)/(\delta T_2)])`

`\delta T_lm = (65 - 25)/(ln [(65)/(25)]) = 41.862`

`P = (Tw_out - Tw_in)/(To_in - Tw_in)`

`P = (55 - 20)/(120 - 20) = 0.35`

`R = (To_in - To_out)/(Tw_out - Tw_in)`

`P = (120 - 45)/(55 - 20) = 2.15`

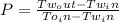
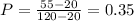
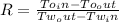
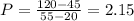
Using the correction factor chart, at P and R = 0.35 and 2.15 respectively, F = 0.7

From the equation, let's make U the subject,

`U = (Q)/(A*F* \delta T_lm)`

`U = (439.8)/(2.714*0.7* 41.862)`

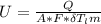
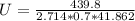
U = 5.53 kW/m² °C