Question

Situation: two electrons, each with mass m and charge q, are released from positions very far from each other. With respect to a certain reference frame, electron A has initial nonzero speed v toward electron B in the positive x direction, and electron B has initial speed 3v toward electron A in the negative x direction. The electrons move directly toward each other along the x axis (very hard to do with real electrons). As the electrons approach each other, they slow due to their electric repulsion. This repulsion eventually pushes them away from each other.

Question: What is the minimum separation r_min that the electrons reach?
Express your answer in term of q, m, v, and k (where k=).
r_min =

Answer 1

min = kq^2/5mv^2

Step-by-step explanation:

The total kinetic energy of both electrons will be electrostatic potential energy, when the electrons reach the minima distance due to electrostatic repulsion. Then, you have:

`E_(k)=U_E\\\\(1)/(2)m_ev_1^2+(1)/(2)m_ev_2^2=k(q^2)/(r_(min))`

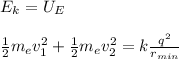
me: mass of the electron

q: charge of the electron

k: Coulomb's constant

you take into account that v2=3v1=3v and do rmin the subject of the formula:

`(1)/(2)m_e[v^2+9v^2]=5m_ev^2=k(q^2)/(r_(min))\\\\r_(min)=(kq^2)/(5m_ev^2)`

hence, the minimum distance between the two electrons is kq^2/5mv^2