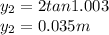Question

A double slit experiment is conducted with a red laser with wavelength l = 700 nm. The distance between the slits and the viewing screen is L = 2.00 m. Consider two experiments that have different slit spacings: Experiment A with dA = 2.00 μm and Experiment B with dB = 40.0 μm. For each experiment, calculate the following (be sure to keep at least three significant figures in all your intermediate calculations):

a) Using Δr = d sinθ , calculate the angle, q1, for the first maximum (constructive interference) above the central maximum. Experiment A and Experiment B
b) Using the angle you calculated in part a) and y = L tanθ , calculate y1, the location on the screen of the first maximum.Experiment A and Experiment B

Answer 1

a)
`\theta_A = 20.49^(0)`,
`\theta_B = 1.003^(0)`

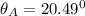b) y1 = 0.75 m, y2 = 0.035 m

Step-by-step explanation:

Wavelength,
`\lambda = 700 nm = 700 * 10^(-9) m`

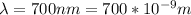
Distance between the slits and the viewing screen, L = 2m

Slit spacing for experiment A,
`d_(A) = 2 \mu m = 2 * 10^(-6) m`

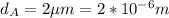
Slit spacing for experiment B,
`d_(B) = 40 \mu m = 40 * 10^(-6) m`

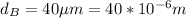
For maximum light intensity,
`n \lambda = d sin \theta`

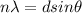
a) For experiment A,
`n \lambda = d_A sin \theta`

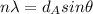
n = 1 ( first maximum )

`700 * 10^(-9) = 2 * 10^(-6) sin \theta_A\\sin \theta_A = (700 * 10^(-9))/(2 * 10^(-6)) \\sin \theta_A = 0.35\\ \theta_A = sin^(-1) 0.35\\\theta_A = 20.49^(0)`

For experiment B,
`n \lambda = d_B sin \theta`

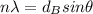
n = 1 ( first maximum )

`700 * 10^(-9) = 40 * 10^(-6) sin \theta_B\\sin \theta_B = (700 * 10^(-9))/(40 * 10^(-6)) \\sin \theta_B = 0.0175\\ \theta_B = sin^(-1) 0.0175\\\theta_B = 1.003^(0)`

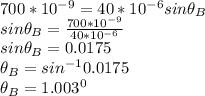
b) The location on the screen of the first maximum:

y = L tanθ

L = 2 m

For experiment A, the location on the screen of the first maximum is calculated as:

`y_1 = L tan \theta_(A)`,
`\theta_A = 20.49^(0)`

`y_1 = 2 tan 20.49\\y_1 = 0.75 m`

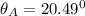
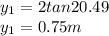
For experiment B, the location on the screen of the first maximum is calculated as:

`y_2 = L tan \theta_(B)`,
`\theta_B = 1.003^(0)`

`y_2 = 2 tan 1.003\\y_2 = 0.035 m`