Answer:
Now if the confidence level increase to 95% then the critical value
 would increase since if we want more confidence the margin of error need's to increase. And since the width for the confidence interval is given by:
would increase since if we want more confidence the margin of error need's to increase. And since the width for the confidence interval is given by:
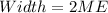
And the margin of error is:
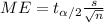
Then we can conclude that increasing the confidence level from 90% to 95% the width of the interval would:
B. Increase
Explanation:
For this case we can define the variable of interest as the number of units for students at their college and we are interested in a confidence interval for the true mean
 and for this parameter the confidence interval is given by this formula:
and for this parameter the confidence interval is given by this formula:
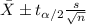
The confidence interval at 90% of confidence is given:
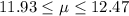
Now if the confidence level increase to 95% then the critical value
 would increase since if we want more confidence the margin of error need's to increase. And since the width for the confidence interval is given by:
would increase since if we want more confidence the margin of error need's to increase. And since the width for the confidence interval is given by:
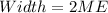
And the margin of error is:
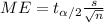
Then we can conclude that increasing the confidence level from 90% to 95% the width of the interval would:
B. Increase