Question

One of the more famous anecdotes in the field of statistics is known as the "Lady Tasting Tea" and involves the renowned Not complete statistician Sir Ronald Aylmer Fisher. A woman claimed to be able to tell the difference in a cup of tea depending on whether or not the milk or tea was poured first. This seemed to be an incredible boast to those in earshot, so Sir Fisher proposed a test. He poured a number of cups of tea, some with tea first and some with milk, first, then randomized the order in which she tasted the cups. (we omit the details here, but it is said that she correctly identified every one!) You have chosen to recreate this experience with a classmate and have fixed 40 cup of tea, of which your classmate correctly identified every one!) You have chosen to recreate this experience with a classmate and have fixed 40 cups of tea, of which your classmate correctly identifies 12. Suppose you wished to see if there is evidence that your classmate is doing worse than would be expected by just guessing. To do this you test the following hypotheses: H_0: p = 0.50, Ha :p < 0.50 The P-value of your test is:_________.

a. between 0.10 and 0.05.
b. between 0.05 and 0.01.
c. between 0.01 and 0.001.
d. below 0.001.

Answer 1

c. between 0.01 and 0.001

Explanation:

Given :

n = 40

x = 12

P = 0.5

H0: p = 0.50

Ha :p < 0.50

Sample proportion, p' =
`(x)/(n) = (12)/(40) = 0.3`

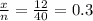
This is a lower tailed test

Standard deviation will be:

`\sigma = \sqrt{(P(1 - P))/(n)} = \sqrt{(0.5(1 - 0.5))/(40)} = 0.0791`

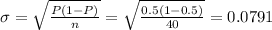
For test statistic :

`= (0.3 - 0.5)/(0.0791) = -2.529 ≈ -2.53`

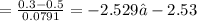
p-value wil be:

(P < Zobserved) = (P < -2.53)

From the normal distribution table,

NORMSDIST(-2.53) = 0.0057060 ≈ 0.0057

p-value = 0.0057

Therefore the p-value is between

c. between 0.01 and 0.001.