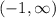Question

Graphs of Function,

Write in interval notation the areas of increase and decrease.
I don't need all of them answered maybe 1 or 2? I want to do some myself.
Thank you for any help on this.

Answer 1

A function is increasing when the gradient is positive

A function is decreasing when the gradient is negative

Question 7

If you draw a tangent to the curve in the interval x < -2 then the tangent will have a positive gradient, and so the function is increasing in this interval.

If you draw a tangent to the curve in the interval x > -2 then the tangent will have a negative gradient, and so the function is decreasing in this interval.

If you draw a tangent to the curve at the vertex of the parabola, it will be a horizontal line, and so the gradient at x = -2 will be zero.

The function is increasing when x < -2

`(- \infty,-2)`

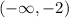
The function is decreasing when x > -2

`(-2, \infty)`

Additional information

We can actually determine the intervals where the function is increasing and decreasing by differentiating the function.

The equation of this graph is:

`f(x)=-2x^2-8x-8`

`\implies f'(x)=-4x-8`

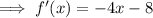
The function is increasing when
`f'(x) > 0`

`\implies -4x-8 > 0`

`\implies -4x > 8`

`\implies x < -2`

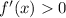
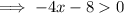
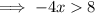
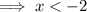
The function is decreasing when
`f'(x) < 0`

`\implies -4x-8 < 0`

`\implies -4x < 8`

`\implies x > -2`

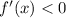
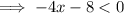
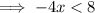
This concurs with the observations made from the graph.

Question 8

This is a straight line graph. The gradient is negative, so:

The function is decreasing for all real values of x

`(- \infty,+ \infty)`

But if they want the interval for the grid only, it would be -4 ≤ x ≤ 1

`[-4,1]`

Question 9

If you draw a tangent to the curve in the interval x < -1 then the tangent will have a negative gradient, and so the function is decreasing in this interval.

If you draw a tangent to the curve in the interval x > -1 then the tangent will have a positive gradient, and so the function is increasing in this interval.

If you draw a tangent to the curve at the vertex of the parabola, it will be a horizontal line, and so the gradient at x = -1 will be zero.

The function is decreasing when x < -1

`(- \infty,-1)`

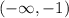
The function is increasing when x > -1

`(-1, \infty)`