Answer:
We conclude that there is no difference in the proportion of cockroaches that died on each surface.
Step-by-step explanation:
We are given that a study investigated the persistence of this pesticide on various types of surfaces.
After 14 days, they randomly assigned 72 cockroaches to two groups of 36, placed one group on each surface, and recorded the number that died within 48 hours. On the glass, 18 cockroaches died, while on plasterboard, 25 died.
Let
 = proportion of cockroaches that died on glass surface.
= proportion of cockroaches that died on glass surface.
 = proportion of cockroaches that died on plasterboard surface.
= proportion of cockroaches that died on plasterboard surface.
So, Null Hypothesis,
 :
:
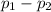 = 0 {means that there is no difference in the proportion of cockroaches that died on each surface}
= 0 {means that there is no difference in the proportion of cockroaches that died on each surface}
Alternate Hypothesis,
 :
:
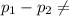 0 {means that there is a significant difference in the proportion of cockroaches that died on each surface}
0 {means that there is a significant difference in the proportion of cockroaches that died on each surface}
The test statistics that would be used here Two-sample z proportion statistics;
T.S. =
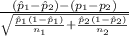 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of cockroaches that died on glass surface =
= sample proportion of cockroaches that died on glass surface =
 = 0.50
= 0.50
 = sample proportion of cockroaches that died on plasterboard surface =
= sample proportion of cockroaches that died on plasterboard surface =
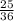 = 0.694
= 0.694
 = sample of cockroaches on glass surface = 36
= sample of cockroaches on glass surface = 36
 = sample of cockroaches on plasterboard surface = 36
= sample of cockroaches on plasterboard surface = 36
So, test statistics =
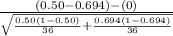
= -1.712
The value of z test statistics is -1.712.
Since, in the question we are not given with the level of significance so we assume it to be 5%. Now, at 5% significance level the z table gives critical values of -1.96 and 1.96 for two-tailed test.
Since our test statistics lies within the range of critical values of z, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.
Therefore, we conclude that there is no difference in the proportion of cockroaches that died on each surface.