Question

In a study of cell phone usage and brain hemispheric​ dominance, an Internet survey was​ e-mailed to 6964 subjects randomly selected from an online group involved with ears. There were 1299 surveys returned. Use a 0.01 significance level to test the claim that the return rate is less than​ 20%. Use the​ P-value method and use the normal distribution as an approximation to the binomial distribution.

Answer 1

We conclude that the return rate is less than​ 20%.

Explanation:

We are given that in a study of cell phone usage and brain hemispheric​ dominance, an Internet survey was​ e-mailed to 6964 subjects randomly selected from an online group involved with ears.

There were 1299 surveys returned.

Let p = return rate.

So, Null Hypothesis,
`H_0` : p
`\geq` 20% {means that the return rate is more than​ or equal to 20%}

Alternate Hypothesis,
`H_0` : p < 20% {means that the return rate is less than​ 20%}

The test statistics that would be used here One-sample z proportion statistics;

T.S. =
`\frac{\hat p-p}{\sqrt{(\hat p(1-\hat p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion of surveys returned =
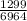`(1299)/(6964)` = 0.186

n = sample of subjects = 6964

So, test statistics =
`\frac{0.186-0.20}{\sqrt{(0.186(1-0.186))/(6964) } }`

= -2.88

The value of z test statistics is -2.88.

Now, P-value of the test statistics is given by the following formula;

P-value = P(Z < -2.88) = 1 - P(Z
`\leq` 2.88)

= 1 - 0.99801 = 0.00199

Since, the P-value of test statistics is less than the level of significance as 0.00199 < 0.01, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the return rate is less than​ 20%.