Question

a band of 45 ewoks crash-landed in the forest last night. this sounds like a small problem, but the population will grow at the rate of 22% per year. write an equation to describe the population in any given year. also, create a table that shows that you walk population every five years from this year to the year 2050

Answer 1

Given Information:

Starting population = P₀ = 45

rate of growth = 22%

Required Information:

Population every five years from this year to the year 2050 = ?

Answer:

`Year \: 2020 = P(0) = 45e^(0) = 45\\\\Year \: 2025 = P(5) = 45e^(0.22*5) = 135\\\\Year \: 2030 = P(10) = 45e^(0.22*10) = 406\\\\Year \: 2035 = P(15) = 45e^(0.22*15) = 1,220\\\\Year \: 2040 = P(20) = 45e^(0.22*20) = 3,665\\\\Year \: 2045 = P(25) = 45e^(0.22*25) = 11,011\\\\Year \: 2050 = P(30) = 45e^(0.22*30) = 33,079\\\\`

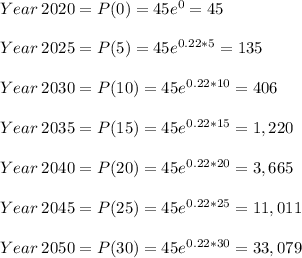
Explanation:

The population growth can be modeled as an exponential function,

`P(t) = P_0e^(rt)`

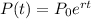
Where P₀ is the starting population, r is the rate of growth of the population and t is the time in years.

We are given that starting population of 45 and growth rate of 22%

`P(t) = 45e^(0.22t)`

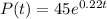
Assuming that the starting year is 2020,

`Year \: 2020 = P(0) = 45e^(0) = 45\\\\Year \: 2025 = P(5) = 45e^(0.22*5) = 135\\\\Year \: 2030 = P(10) = 45e^(0.22*10) = 406\\\\Year \: 2035 = P(15) = 45e^(0.22*15) = 1,220\\\\Year \: 2040 = P(20) = 45e^(0.22*20) = 3,665\\\\Year \: 2045 = P(25) = 45e^(0.22*25) = 11,011\\\\Year \: 2050 = P(30) = 45e^(0.22*30) = 33,079\\\\`

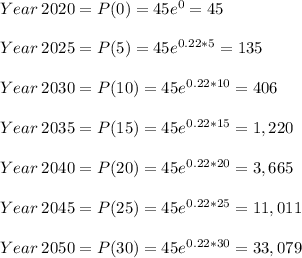
Therefore, the starting population of ewoks was 45 in 2020 and increased to 33,079 by 2050 in a time span of 30 years.