We have been given that a bag contains 2 red marbles and 3 black marbles. Abby picks a marble without looking, returns it to the bag, and then draws a second marble. We are asked to find the probability that both marbles are red.
Let
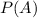 be probability of getting a red marble on 1st draw and
be probability of getting a red marble on 1st draw and
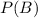 be probability of getting a red marble on 2nd draw.
be probability of getting a red marble on 2nd draw.
Number of red marbles = 2
Total number of marbles =
 .
.
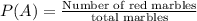

Since Abby returns the marble into the bag, so number of marbles will not change. This means that probability of both events is independent.


When two events are independent, then their probability is
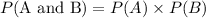
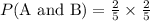
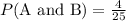
Therefore, the probability that both marbles are red would be
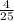 .
.