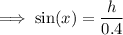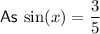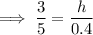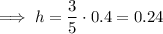Question

Find the length of h. Round to the nearest hundreth.​

Answer 1

• x=y=z

Remember (3,4,5) Pythagorean triplet

Triangle containing y

• Hypotenuse=0.5
• Base=0.4

Triangle containing x

• Base=0.4
• Perpendicular=0.3

Now use ratio to find

• 0.5/0.3=0.4/h
• 5/3=0.4/h
• 5h=1.2
• h=1.2/5
• h=0.24

Answer 2

h = 0.24

Explanation:

Assuming this is a parallelogram...

Sine trig ratio

`\sin(\theta)=\sf (O)/(H)`

where:

• 
  `\theta` is the angle
• O is the side opposite the angle
• H is the hypotenuse

Let x be the angle in the top left of the parallelogram.

`\implies \sin(x)=(0.3)/(0.5)=\frac35`

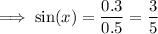
Opposite angles in a parallelogram are congruent.

Therefore, the angle in the bottom right of the parallelogram is also x.

`\implies \sin(x)=(h)/(0.4)`

`\textsf{As} \:\sin(x)=\frac35`

`\implies \frac35=(h)/(0.4)`

`\implies h=\frac35 \cdot 0.4=0.24`