Answer:
Explanation:
We are going to consider the inner product
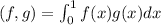
Consider the following trigonometric identity:
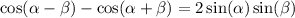
Suppose that
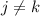 consider the inner product and the identity:
consider the inner product and the identity:
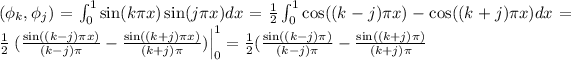
Note that since k,j are integers then k-j and k+j are integers. Then, by properties of the sine function we have that
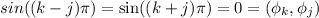
Consider also the following identity:
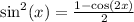
Suppose that j=k. Then
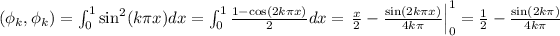
Since k is an integer, then
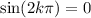 . So
. So

This proves what's been asked in the question.