Question

Which statement justifies that 3x² − 2x − 4 multiplied by 2x² + x − 3 obeys the closure property of multiplication?

The result 6x⁴ − 2x² + 12 has a degree of 4.
The result 6x⁴ − 2x² + 12 is a trinomial.
The result 6x⁴ − x³ − 19x² + 2x + 12 is a polynomial.
The result 6x⁴ − x³ − 19x² + 2x + 12 has a degree of 4.

Answer 1

Explanation:

(3x2 - 2x - 4) (2x2 + x - 3)

6x4 + 3x3 - 9x2 - 4x3 - 2x2 + 6x - 8x2 - 4x + 12

Solving like terms

6x4 - x3 - 19x2 + 2x + 12

Answer 2

C) The result 6x⁴ − x³ − 19x² + 2x + 12 is a polynomial.

Explanation:

We have been given two polynomials
`3x^2-2x -4 \text{ and } 2x^2+x-3`.

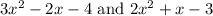Let us first multiply these polynomials.

`(3x^2 - 2x - 4)(2x^2 + x - 3) \\= 3x^2(2x^2 + x - 3) -2x(2x^2 + x - 3)-4(2x^2 + x - 3)\\=6 x^4 - x^3 - 19 x^2 + 2 x + 12`

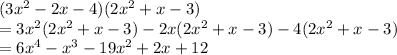
Now, we know that polynomials follows closure property of multiplication, we can come to the conclusion that when we multiply the two polynomials, the result will be a polynomial.

Since, when we multiplied the given polynomials, we got
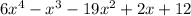`6 x^4 - x^3 - 19 x^2 + 2 x + 12` which is a polynomial.

Therefore, the correct option is:

C) The result 6x⁴ − x³ − 19x² + 2x + 12 is a polynomial.