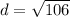Answer:
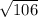 is the length of AT
is the length of AT
Explanation:
To find the length of AT you have to use the distance formula which is
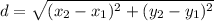
So we have the points (0,0) and (5,9)
All we have to do is substitute the points into the equation
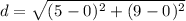
You then get
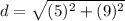
Then square the values and then add them
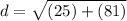
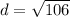
Then simplify what is in the radical, in this case that is all you can do
Your final answer is