Graph a parabola whose x-intercepts are at x = -3 and x = 5 and whose minimum value is y = -4.

Question

asked Jul 2, 2021 52.1k views

2 Answers

Trrrrrrm · Answer 1 · 2021-07-07T19:42:17+0000

Answer:

(See explanation and attachment below for further details)

Explanation:

The parabola must satisfy the following conditions:

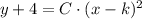
$y + 4 = C\cdot (x - k)^(2)$

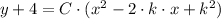
$y + 4 = C\cdot (x^(2)-2\cdot k \cdot x + k^(2))$

The expression for the x-intercepts are, respectively:

x = -3

$4 = C\cdot [(-3)^(2) - 2\cdot k\cdot (-3)+k^(2)]$

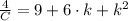
$(4)/(C) = 9 + 6\cdot k + k^(2)$

x = 5

$4 = C\cdot [5^(2)-2\cdot k \cdot (5)+k^(2)]$

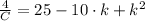
$(4)/(C) = 25 - 10\cdot k + k^(2)$

By equalizing both expressions:

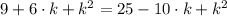
$9 + 6\cdot k + k^(2) = 25 - 10\cdot k + k^(2)$

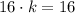
$16\cdot k = 16$

k = 1

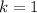
And,

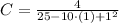
$C = (4)/(25-10\cdot (1)+1^(2))$

C = (1)/(4)

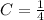
The equation of parabola is:

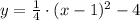
$y = (1)/(4)\cdot (x-1)^(2) - 4$

Whose graph is included as attachment.