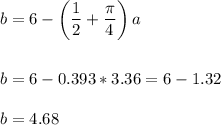Answer:
bottom side (a) = 3.36 ft
lateral side (b) = 4.68 ft
Explanation:
We have to maximize the area of the window, subject to a constraint in the perimeter of the window.
If we defined a as the bottom side, and b as the lateral side, we have the area defined as:
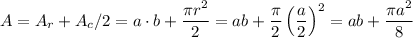
The restriction is that the perimeter have to be 12 ft at most:
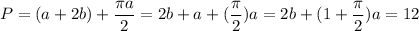
We can express b in function of a as:
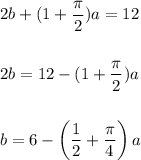
Then, the area become:
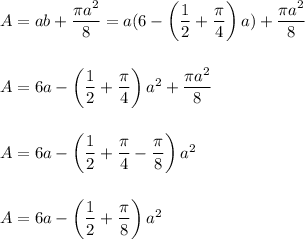
To maximize the area, we derive and equal to zero:
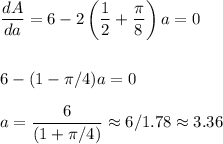
Then, b is: