Question

Loretta, who turns 91 this year, has heard that the mean systolic blood pressure among the elderly is 115 millimeters of mercury (mmHg), but she believes that the actual value is higher. She bases her belief on a recently reported study of 14 randomly selected, elderly adults. The sample mean systolic blood pressure of the adults in the study was 120 mmHg, and the sample standard deviation was 20 mmHg. Assume that the population of systolic blood pressures of elderly adults is normally distributed.

Perform a one-tailed test. Then fill in the blanks below.
Carry your intermediate computations to at least three decimal places and round your answers as specified in the table. (If necessary, consult a list of formulas.)
1) The null hypothesis: H0: _____.
2) The alternative hypothesis: H1: _____.
3) The type of test statistic: _____.
4) The value of the test statistic: _____. (Round to at least three decimal places.)
5) The critical value at the 0.05 level of significance: _____. (Round to at least three decimal places.)
6) Can it be concluded, at the 0.05 level of significance, that the mean systolic blood pressure among elderly adults is greater than 115 mmHg?

Answer 1

1) The null hypothesis: H0: μ=115.

2) The alternative hypothesis: H1: μ>115.

3) The type of test statistic: t-statistic.

4) The value of the test statistic: t=0.935. (Round to at least three decimal places.)

5) The critical value at the 0.05 level of significance: tc=2.160. (Round to at least three decimal places.)

6) Can it be concluded, at the 0.05 level of significance, that the mean systolic blood pressure among elderly adults is greater than 115 mmHg?

No. There is not enough evidence to support the claim that the the actual value of the systolic pressure among the elderly is higher than 115 mmHg (P-value=0.183).

Explanation:

This is a hypothesis test for the population mean.

The claim is that the the actual value of the systolic pressure among the elderly is higher than 115 mmHg.

Then, the null and alternative hypothesis are:

`H_0: \mu=115\\\\H_a:\mu> 115`

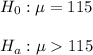
The significance level is 0.05.

The sample has a size n=14.

The sample mean is M=120.

As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=20.

The estimated standard error of the mean is computed using the formula:

`s_M=(s)/(√(n))=(20)/(√(14))=5.345`

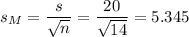
Then, we can calculate the t-statistic as:

`t=(M-\mu)/(s/√(n))=(120-115)/(5.345)=(5)/(5.345)=0.935`

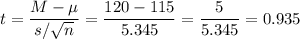
The degrees of freedom for this sample size are:

`df=n-1=14-1=13`

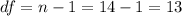
This test is a right-tailed test, with 13 degrees of freedom and t=0.935, so the P-value for this test is calculated as (using a t-table):

`P-value=P(t>0.935)=0.183`

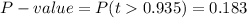
As the P-value (0.183) is bigger than the significance level (0.05), the effect is not significant.

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that the the actual value of the systolic pressure among the elderly is higher than 115 mmHg.

The critical value for a significance level of 0.05 and 13 degrees of freedom is tc=2.160.