Question

Test the claim that the mean GPA of night students is larger than 3.1 at the .10 significance level. The null and alternative hypothesis would be:

H 0 : μ = 3.1 H 1 : μ < 3.1
H 0 : μ = 3.1 H 1 : μ ≠ 3.1
H 0 : p = 0.775 H 1 : p > 0.775
H 0 : μ = 3.1 H 1 : μ > 3.1
H 0 : p = 0.775 H 1 : p ≠ 0.775
H 0 : p = 0.775 H 1 : p < 0.775
The test is:
two-tailed
right-tailed
left-tailed
Based on a sample of 75 people, the sample mean GPA was 3.13 with a standard deviation of 0.03.
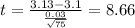
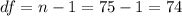
The p-value is:_______.
The significance level is:_______.
Based on this we:
Reject the null hypothesis
Fail to reject the null hypothesis

Answer 1

H 0 : μ = 3.1 H 1 : μ > 3.1

And this test is defined a a right tailed test since the symbol for the alternative hypothesis H1 is >.

`t = (3.13-3.1)/((0.03)/(√(75)))= 8.66`

`df = n-1=75-1 =74`

The p value is:

`p_v = P(t_(74) >8.66) =3.65x10^(-13)`

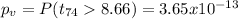
The significance level is: 0.1 or 10%

And since the p value is very low compared to the significance level we have enough evidence to:

Reject the null hypothesis

Explanation:

For this case we want to test the claim that mean GPA of night students is larger than 3.1 at the .10 significance level. The claim needs to be on the alternative hypothesis so then we have the following system of hypothesis:

H 0 : μ = 3.1 H 1 : μ > 3.1

And this test is defined a a right tailed test since the symbol for the alternative hypothesis H1 is >.

We have the following info given:

`\bar X = 3.13 , s =0.03 , n =75`

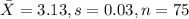
The statistic to check the hypothesis is given by:

`t = (\bar X -\mu)/((s)/(√(n)))`

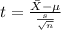
Replacing the info given we got:

`t = (3.13-3.1)/((0.03)/(√(75)))= 8.66`

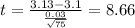
The degrees of freedom are given by:

`df = n-1=75-1 =74`

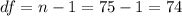
The p value since is a right tailed ted is given by:

`p_v = P(t_(74) >8.66) =3.65x10^(-13)`

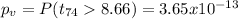
The significance level is 0.1 or 10%

And since the p value is very low compared to the significance level we have enough evidence to:

Reject the null hypothesis