Question

Medical researchers have devised a test that quantitatively meaasures a person's risk of heart disease. The test scores for the general public are approximately normally distributed with a mean of 50. On the test, higher test scores indicate a higher risk of heart disease. An advocate of long distance running believes that marathon runners should have a lower risk of heart disease than the general public. A random sample of 20 marathon runners is selected and each is tested for their risk of heart disease. Their test scores have a mean of 43.7 and a standard deviation of 4.2. Construct a 90% confidence interval for u, the true mean score for all marathon runners.

a. 43.7 + 1.62.
b. 43.7 + 6.91.
c. 43.7 + 0.94.
d. 43.7 + 4.2.
e. 43.7 + 8.40.

Answer 1

`df = n-1=20-1=19`

The confidence level for this case is 90% so then the significance level is
`\alpha=0.1` and
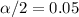`\alpha/2 =0.05` so then the critical value in the t distribution with df =19 is given by :

`t_(\alpha/2)= 1.729`

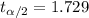
Now we can find the margin of error for the confidence interval given by:

`ME = t_(\alpha/2)(s)/(√(n))`

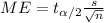
And replacing we got:

`ME = 1.729 *(4.2)/(√(20))= 1.624`

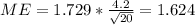
And the confidence interval would be given by:

`43.7 \pm 1.62`

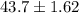
And the best option is:

a. 43.7 + 1.62.

Explanation:

The random variable of interest for this problem is the score for all marathon runners X and in special we want to infer about the true mean
`\mu`. We have the following info given:

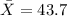`\bar X= 43.7` the sample mean for the test scores

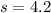`s= 4.2` the sample deviation given

`n = 20` the sample size selected

And we want to construct a confidence interval for the true mean given by this formula:

`\bar X \pm t_(\alpha/2)(s)/(√(n))`

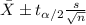
The degrees of freedom for this case are given by:

`df = n-1=20-1=19`

The confidence level for this case is 90% so then the significance level is
`\alpha=0.1` and
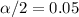`\alpha/2 =0.05` so then the critical value in the t distribution with df =19 is given by :

`t_(\alpha/2)= 1.729`

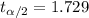
Now we can find the margin of error for the confidence interval given by:

`ME = t_(\alpha/2)(s)/(√(n))`

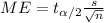
And replacing we got:

`ME = 1.729 *(4.2)/(√(20))= 1.624`

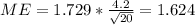
And the confidence interval would be given by:

`43.7 \pm 1.62`

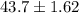
And the best option is:

a. 43.7 + 1.62.