Question

Verifique se o ponto P(2 , 3) pertence à reta r que passsa pelos pontos A(1 , 1) e B(0 , -3).

Answer 1

The point P does not belong to the line that passes through points A and B.

Explanation:

P is inside line AB only line AP is a multiple of the line AB. That is:

`\vec l_(AP) = \alpha \cdot \vec l_(AB)`

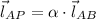
Vectorially speaking, the line AB is equal to:

`\vec l_(AB) = (0-1,-3-1)`

`\vec l_(AB) = (-1,-4)`

The vector form of the line AP is:

`\vec l_(AP) = (2-1,3-1)`

`\vec l_(AP) = (1, 2)`

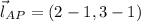
The following property must be fulfilled:

`(x_(2),y_(2)) = (\alpha \cdot x_(1),\alpha \cdot y_(1))`

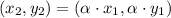
The coefficients of each component are computed:

`\alpha_(x) = (1)/(-1)`

`\alpha_(x) = -1`

`\alpha_(y) = (2)/(-4)`

`\alpha_(y) = -(1)/(2)`

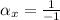
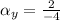
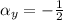
Since
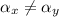`\alpha_(x) \\eq \alpha_(y)`, the point P does not belong to the line that passes through points A and B.