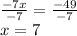Question

Tickets for a play cost $3 for children and $10 for adults. A group of 25 people paid a total of $201 for tickets to the play. How many children were in a group?

Answer 1

7 children.

Explanation:

Let c = children

Let a = adults

1) We can set up two equations and solve them simultaneously using substitution or elimination method.

c + a = 25

3c + 10a = 201

2) I will use substitution. Make one of the variables the subject; then, substitute it into the other equation.

a = 25 - c

3c + 10(25 - c) = 201

3) Solve for c; then, substitute it into one of the equations.

3c + 250 - 10c = 201

-7c = 201 - 250

-7c = -49

c = -49/-7

c = 7

Let's substitute it into one of the equations.

7 + a = 25

a = 25 - 7

a = 18

Since the question only asked for the number of children, the answer is 7.

Answer 2

Answer: There were 7 children

Explanation:

Let's use x to represent the children and y to represent the adults.

We know they combine to make a group of 25 people so x+y=25

We also know that they paid $201 and that there is $3 per child and $10 for adults so 3x+10y=201

I will solve by substitution.

Solve for y in the first equation

`x+y=25\\x-x+y=25-x\\y=25-x`

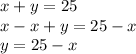
Sub in our value for y into the other equation and solve for x

`3x+10y=201\\3x+10(25-x)=201`

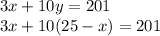
Step 1) Simplify

`3x+250-10x=201\\-7x+250=201`

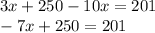
Step 2) Subtract 250 from both sides

`-7x+250-250=201-250\\-7x=-49`

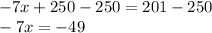
Step 3) Divide both sides by -7

`(-7x)/(-7) =(-49)/(-7)\\x=7`