Answer:
Residual = -2
The negative residual value indicates that the data point lies below the regression line.
Explanation:
We are given a linear regression model that relates daily high temperature, in degrees Fahrenheit and number of lemonade cups sold.
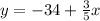
Where y is the number of cups sold and x is the daily temperature in Fahrenheit.
Residual value:
A residual value basically shows the position of a data point with respect to the regression line.
A residual value of 0 is desired which means that the regression line best fits the data.
The Residual value is calculated by
Residual = Observed value - Predicted value
The predicted value of number of lemonade cups is obtained as
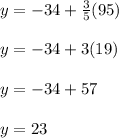
So the predicted value of number of lemonade cups is 23 and the observed value is 21 so the residual value is
Residual = Observed value - Predicted value
Residual = 21 - 23
Residual = -2
The negative residual value indicates that the data point lies below the regression line.