Question

A wire lying along a y axis form y=0 to y=0.25 m carries a current of 2.0 mA in the negative direction of the axis. The wire fully lies in a magnetic field given by (0.3y)i + (0.4y)j Tesla. What isThe magnetic force on the wire

Answer 1

FB = 0.187 N

Step-by-step explanation:

To find the magnetic force FB in the wire you use the following formula:

`|\vec{F_B}|=ILBsin\theta\\\\L=0.25m\\\\|\vec{B}|=√((0.3y)^2+(0.4y)^2)=0.5y \ T`

the angle between B and L is given by:

`\vec{L}\cdot\vec{B}=LBcos\theta\\\\\theta=cos^(-1)(\frac{\vec{L}\cdot\vec{B}}{LB})=cos^(-1)((0*0.3y+0.25*0.4y)/(0.25*0.5y))=36.86\°`

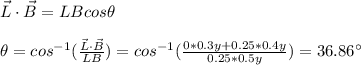
Due to B depends on "y" you take into account the contribution of each element dy of the wire to the magnitude of the magnetic force. Thus, you have to integrate the following expression:

`|\vec{F_B}|=Isin\theta\int_0^(0.25)B(y)dy=Isin\theta\int_0^(0.25)(0.5y)dy\\\\|\vec{F_B}|=(2.0*10^(-3)A)(sin36.86\°)(0.5T)[(0.25^2)/(2)m]=0.187\ N`

hence, the magnitude of the magnetic force is 0.187N