Answer:
3.5 in (nearest tenth)
Explanation:
Properties of a rhombus:
- Quadrilateral (four sides & four interior angles)
- Parallelogram (opposite sides are parallel)
- All sides are equal in length
- Opposite angles are equal in measure
- Diagonals bisect each other at right angles
- Interior angles sum to 360°
- Adjacent angles are supplementary (sum to 180°)
- Diagonals bisect interior angles
Therefore, a rhombus is made up of 4 congruent right triangles.
** see attached diagram **
To find the side length of the rhombus, we need to calculate the hypotenuse of the right triangle.
As the shorter diagonal is 4 in, the base of the right triangle is 2 in
The angles that measure 110° are the angles by the shorter diagonal. Therefore, the base angle of the right triangle is 55°
Using cos trig ratio:
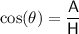
where:
 is the angle
is the angle- A is the side adjacent the angle
- H is the hypotenuse
Given:
 = 55°
= 55°- A = 2
- H = x

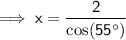
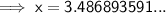
Therefore, the side of the rhombus is 3.5 in (nearest tenth)