Question

If 1/(a + b + c) = 1/a + 1/b + 1/c, show that 1/(a + b + c)^3 = 1/a^3 + 1/b^3 + 1/c^3​

Answer 1

Expanding the cube, we have

`\frac1{(a+b+c)^3} = \left(\frac1{a+b+c}\right)^3 \\\\ = \frac1{a^3} + \frac1{b^3} + \frac1{c^3} + 3 \left(\frac1{a^2b} + \frac1{a^2c} + \frac1{ab^2} + \frac1{b^2c} + \frac1{ac^2} + \frac1{bc^2}\right) + \frac6{abc}`

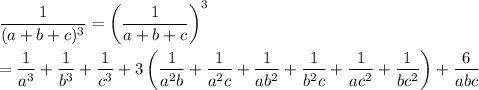
so it remains to be shown that

`3 \left(\frac1{a^2b} + \frac1{a^2c} + \frac1{ab^2} + \frac1{b^2c} + \frac1{ac^2} + \frac1{bc^2}\right) + \frac6{abc} = 0`

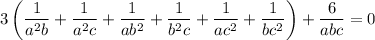
Factorize the grouped sum on the left as

`\frac1{a^2b} + \frac1{a^2c} + \frac1{ab^2} + \frac1{b^2c} + \frac1{ac^2} + \frac1{bc^2} = \frac1{abc} \left(\frac ca + \frac ba + \frac cb + \frac ab + \frac bc + \frac ac\right)`

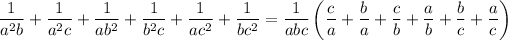
so that with simplification, it remains to be shown that

`\frac ca + \frac ba + \frac cb + \frac ab + \frac bc + \frac ac + 2 = 0`

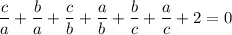
With a little more manipulation, we have

`\frac ba + \frac ca = \frac{a+b+c}a - 1`

`\frac cb + \frac ab = \frac{a+b+c}b - 1`

`\frac bc + \frac ac = \frac{a+b+c}c - 1`

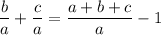
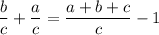
so that our equation simplifies to

`\frac{a+b+c}a + \frac{a+b+c}b + \frac{a+b+c}c - 1 = 0`

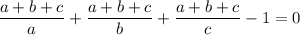
which we can factorize as

`(a+b+c)\left(\frac1a+\frac1b+\frac1c\right) - 1 = 0`

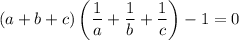
Finish up by using the hypothesis:

`\left(\frac1{\frac1{a+b+c}}\right)\left(\frac1a+\frac1b+\frac1c\right) - 1 = 0`

`\underbrace{\left(\frac1{\frac1a+\frac1b+\frac1c}\right)\left(\frac1a+\frac1b+\frac1c\right)}_(=1) - 1 = 0`

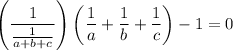
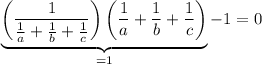
and the conclusion follows.