Answer:
If the volume of the container is decreased to 90.0 ml and the pressure is increased to 1.60 atm the temperature will be 302 °K
Step-by-step explanation:
Boyle's law says that "The volume occupied by a given gas mass at constant temperature is inversely proportional to the pressure", which is expressed mathematically as:
P * V = k
Charles's Law consists of the relationship between the volume and temperature of a certain amount of ideal gas, which is maintained at a constant pressure, by means of a proportionality constant that is applied directly. In summary, Charles's law is a law that says that when the amount of gas and pressure are kept constant, the ratio between volume and temperature will always have the same value:

Finally, Gay Lussac's law establishes that as the temperature increases, the gas molecules move more quickly and therefore the number of collisions against the walls increases, that is, the pressure increases since the container is of fixed walls and its volume can not change. Therefore, the ratio of pressure to temperature always has the same value (it is constant).
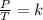
Combined law equation is the combination of three gas laws called Boyle's, Charlie's and Gay-Lusac's law:

Having a state 1 at the beginning and a state 2 at the end is fulfilled:
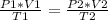
In this case, you know:
- P1= 0.800 atm
- V1= 180 mL= 0.180 L (being 1 L=1000 mL)
- T1= 29 °C= 302 °K
- P2= 1.60 atm
- V2= 90 mL= 0.09 L
- T2=?
Replacing:
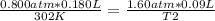
Solving:
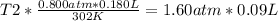

T2= 302 °K
If the volume of the container is decreased to 90.0 ml and the pressure is increased to 1.60 atm the temperature will be 302 °K