Question

A polynomial function has a root of -6 with a multiplicity 1, a root of -2 with multiplicity 3, a root of 0 with a multiplicity 2, and a root od 4 with multiplicity 3. If the function has a positive leading coefficient and is of odd degree, which statement about the graph is true?

Answer 1

According to the given information, the polymomial expression should have the following factors.

Root of -6 and multiplicity of 1:
`(x+6)`

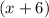
Root of -2 and multiplicity of 3:
`(x+2)^(3)`

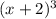
Root of 0 with a multiplicity of 2:
`x^(2)`

Root of 4 and multiplicity of 3:
`(x-4)^(3)`

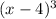
If we sum exponents, we can know the grade of the polnomial:

1 + 3 + 2 + 3 = 9

So, the grade of the polynomial function is 9, which makes it an odd function.

Additionally, the function is

`f(x)=(x+6)x^(2)(x+2)^(3)(x-4)^(3)`

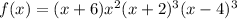
Its graph is attached.