Answer:
A. 1/220 B. 1/22 C. 3/11
Explanation:
This question uses combinations -- counting the number of ways a selection can be made from a set of objects (without arranging them after the selection is done).
Notations for combinations:
The number of ways to select r things from a set of n things is
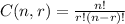 where the exclamation points mean factorial.
where the exclamation points mean factorial.
 and 0! is defined to be 1.
and 0! is defined to be 1.
There are two other commonly used symbols for this:
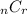 and
and
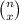 .
.
In all three parts, the number of ways to choose 3 balls from a set of 12 is
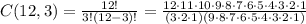
Notice that 9 factors in the denominator cancel 9 factors in the numerator, leaving
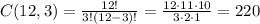
A. The number of ways to choose 3 red balls from the 3 red balls is C(3, 3) = 1, so the probability is 1 / 220.
B) The number of ways to choose 3 green balls from the set of 5 green balls is
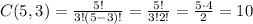 out of 220, so the probability is 10/220 = 1/22.
out of 220, so the probability is 10/220 = 1/22.
C) The number of ways to choose 1 red is C(3, 1) = 3. Choose 1 green in C(5, 1) = 5 ways. Choose 1 white in C(4, 1) = 4 ways.
The probability is
