Question

Geometry 100 points!

Answer 1

-1, -1 is on the line equation y = 4/3x + 1/3

Explanation:

formula = y = mx + c

1. (- 1, -1)

-1 = 4/3. -1 + 1/3

-1 = -1 -> fulfill

2. (0,0)

0 = 4/3. 0 + 1/3

0 = 1/3 -> do not meet

3. (3,3)

3 = 4/3. 3 + 1/3

3 = 4 1/3 -> do not meet

4. (1,1)

1 = 4/3. 1 + 1/3

1 = 5/3 -> do not meet

So the point that meets is point -1, -1

Answer 2

(-1, -1)

Explanation:

Given equation of the perpendicular transversal:

`y=(4)/(3)x+(1)/(3)`

To find which ordered pair would be on the perpendicular transversal, simply input each value of x into the equation:

`\begin{aligned}x=-1 \implies y&=(4)/(3)(-1)+(1)/(3)\\&=-(4)/(3)+(1)/(3)\\&=(-4+1)/(3)\\&=(-3)/(3)\\&=-1\end{aligned}`

`\begin{aligned}x=0 \implies y&=(4)/(3)(0)+(1)/(3)\\&=0+(1)/(3)\\&=(1)/(3)\end{aligned}`

`\begin{aligned}x=3 \implies y&=(4)/(3)(3)+(1)/(3)\\&=(12)/(3)+(1)/(3)\\&=(12+1)/(3)\\&=(13)/(3)\end{aligned}`

`\begin{aligned}x=1 \implies y&=(4)/(3)(1)+(1)/(3)\\&=(4)/(3)+(1)/(3)\\&=(4+1)/(3)\\&=(5)/(3)\end{aligned}`

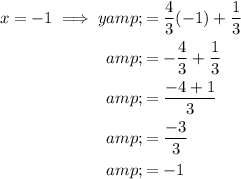
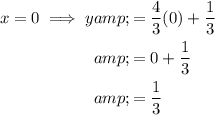
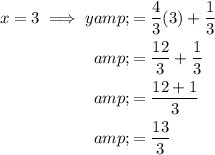
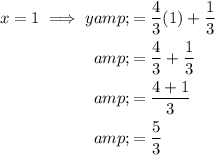
Therefore, the only ordered pair that is on the perpendicular transversal is:

• (-1, -1)