Question

The prices of commodities X,Y,Z are respectively x, y, z, rupees per unit. Mr. A purchases 4 units of Z and sells 3 units of X and 5 units of Y. Mr. B purchases 3 units of Y and sells 2 units of X and 1 units of Z. Mr. C purchases 1 units of X and sells 4 units of Y and 6 units of Z.in this process A and C earn Rs. 6000 and Rs. 13000 respectively. While B neither lose nor gain. Find the prices per unit of the three commodities by using appropriate method.

please help me!!

Answer 1

`(x,y,z)=(1477, 1464, 1437)`

Explanation:

Consider the selling of the units positive earning and the purchasing of the units negative earning.

Case-1:

• Mr. A purchases 4 units of Z and sells 3 units of X and 5 units of Y
• Mr.A earns Rs6000

So, the equation would be

`3x + 5y - 4z = 6000`

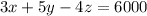
Case-2:

• Mr. B purchases 3 units of Y and sells 2 units of X and 1 units of Z
• Mr B neither lose nor gain meaning he has made 0₹

hence,

`2x - 3y + z = 0`

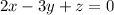
Case-3:

• Mr. C purchases 1 units of X and sells 4 units of Y and 6 units of Z
• Mr.C earns 13000₹

therefore,

`- x + 4y + 6z = 13000`

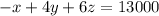
Thus our system of equations is

`\begin{cases}3x + 5y - 4z = 6000\\2x - 3y + z = 0\\ - x + 4y + 6z = 13000\end{cases}`

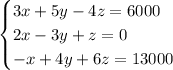
Solving the system of equations:

we will consider elimination method to solve the system of equations. To do so ,separate the equation in two parts which yields:

`\begin{cases}3x + 5y - 4z = 6000\\2x - 3y + z = 0\end{cases}\\\begin{cases}2x - 3y + z = 0\\ - x + 4y + 6z = 13000\end{cases}`

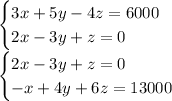
Now solve the equation accordingly:

`\implies\begin{cases}11x-7y=6000\\-13x+22y=13000\end{cases}`

Solving the equation for x and y yields:

`\implies\begin{cases}x= (223000)/(151)\\\\y= (221000)/(151)\end{cases}`

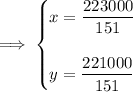
plug in the value of x and y into 2x - 3y + z = 0 and simplify to get z. hence,

`\implies z= (217000)/(151)`

Therefore,the prices of commodities X,Y,Z are respectively approximately 1477, 1464, 1437