Question

This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part.

Find a power series representation for the function. Determine the interval of convergence. (Give your power series representation centered at x=0)
f(x)=1/6+x

Answer 1

The series representation is
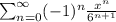`\sum_(n=0)^(\infty)(-1)^n(x^n)/(6^(n+1))` and the interval of convergence is (-6,6)

Explanation:

We want to find a series, such that f(x) = \sum_{n=0}{\infty}a_n(x-a)^{n}[/tex], were a is the value that we are using to center the series expansion. In our case, a=0.

We will use the geometric series formula as follows. For |r|<1 then

`(1)/(1-r)=\sum_(n=0)^(\infty) r^n`

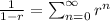
In our case, with some algebreaic manipulation we have that

`f(x) = (1)/(6+x) = (1)/(6)(1)/(1-((-x)/(6)))`

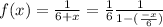
Taking
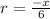`r = (-x)/(6)` we get that

`f(x) = (1)/(6)\sum_(n=0)^(\infty) ((-x)/(6))^n = \sum_(n=0)^(\infty)(-1)^n(x^n)/(6^(n+1))`

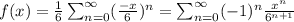
This representation is valid (that means that the series converges to the value of f(x)) only for |r|<1. That is

`\left|(-x)/(6)\right|= \left|(x)/(6)\right|<1`

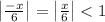
which implies that |x|<6. So the interval of convergence is (-6,6).