Question

Jiffy Mix in Chelsea, Michigan has a machine that fills the Jiffy Corn Muffin Mix boxes with Mix. It dispenses corn muffin mix with a normal distribution and has a mean of 10.0 and a standard deviation of 0.1 ounces.

Part B) The middle 68% of Jiffy Corn Muffin Mix boxes contain between___and___ounces of corn muffin mix.

Part C) What percentage of Jiffy Corn Muffin Mix boxes contain more than 10.3 ounces or less than 9.7 ounces of corn muffin mix?____% of the boxes.

Part D) What percentage of Jiffy Corn Muffin Mix boxes contain more than 10.2 ounces of corn muffin mix?___% of the boxes

Part E) What is the probability that a randomly selected Jiffy Corn Muffin Mix box contains less than 10.1 ounces of corn muffin mix?___% of the boxes

Answer 1

(b) The middle 68% of Jiffy Corn Muffin Mix boxes contain between 9.90 ounces and 10.10 ounces of corn muffin mix.

(c) The percentage of Jiffy Corn Muffin Mix boxes containing more than 10.3 ounces or less than 9.7 ounces of corn muffin mix is 16%.

(d) The percentage of iffy Corn Muffin Mix boxes containing more than 10.2 ounces of corn muffin mix is 2.3%.

(e) The percentage of Jiffy Corn Muffin Mix boxes containing less than 10.1 ounces of corn muffin mix is 84%.

Explanation:

Let the random variable X be defined as the amount of corn muffin mix in a Jiffy Corn Muffin Mix box.

The random variable X follows a Normal distribution with mean, μ = 10.0 ounces and standard deviation, σ = 0.10 ounces.

(b)

According to the Empirical rule, 68% of the data from a Normal distribution lies within one standard deviation of mean.

That is:

P (x₁ < X < x₂) = 0.68

P (μ - σ < Z < μ + σ) = 0.68

Then,

P (10.0 - 0.10 < Z < 10.0 + 0.10) = 0.68

P (9.90 < Z < 10.10) = 0.68

Thus, the middle 68% of Jiffy Corn Muffin Mix boxes contain between 9.90 ounces and 10.10 ounces of corn muffin mix.

(c)

Compute the probability that Jiffy Corn Muffin Mix boxes contain more than 10.3 ounces or less than 9.7 ounces of corn muffin mix as follows:

P (X > 10.3 ∪ X < 9.7) = 1 - P (9.7 < X < 10.3)

`=1-P((9.7-10.0)/(0.10)<(X-\mu)/(\sigma)<(10.10-10.0)/(0.10))\\\\=1-P(-3<Z<1)\\\\=1-[P(Z<1)-P(Z<-3)]\\\\=1-[0.84134-0.00135]\\\\=0.16001\\\\\approx 0.16`

Thus, the percentage of Jiffy Corn Muffin Mix boxes containing more than 10.3 ounces or less than 9.7 ounces of corn muffin mix is 16%.

(d)

Compute the probability of Jiffy Corn Muffin Mix boxes contain more than 10.2 ounces of corn muffin mix as follows:

`P(X>10.2)=P((X-\mu)/(\sigma)>(10.20-10.0)/(0.10))`

`=P(Z>2)\\=1-P(Z<2)\\=1-0.97725\\=0.02275\\\approx 0.023`

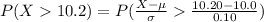
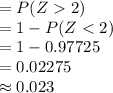
Thus, the percentage of iffy Corn Muffin Mix boxes containing more than 10.2 ounces of corn muffin mix is 2.3%.

(e)

Compute the probability that a randomly selected Jiffy Corn Muffin Mix box contains less than 10.1 ounces of corn muffin mix as follows:

`P(X<10.1)=P((X-\mu)/(\sigma)<(10.1-10.0)/(0.10))`

`=P(Z<1)\\=0.84134\\\approx 0.84`

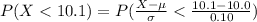
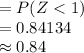
Thus, the percentage of Jiffy Corn Muffin Mix boxes containing less than 10.1 ounces of corn muffin mix is 84%.