Question

if $600 is deposit into an account earning compound interest at an annual rate of 3% for 5 years, and it is compounded quarterly (thus 4 times per year) how much money is in the account at the end of the 5 years?

Answer 1

At the end of 5 years, there will be $696.71 in the account.

Explanation:

The compound interest formula is given by:

`A(t) = P(1 + (r)/(n))^(nt)`

Where A(t) is the amount of money after t years, P is the principal(the initial sum of money), r is the interest rate(as a decimal value), n is the number of times that interest is compounded per unit year and t is the time in years for which the money is invested or borrowed.

In this question, we have that:

`P = 600, r = 0.03, t = 5, n = 4`

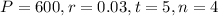
Then

`A(t) = P(1 + (r)/(n))^(nt)`

`A(5) = 600(1 + (0.03)/(4))^(4*5)`

`A(5) = 696.71`

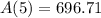
At the end of 5 years, there will be $696.71 in the account.